A Step by Step Guide to Dimensional Analysis

When working a dimensional analysis, or unit factor problem, keep the following in mind:

• Don't panic.
• Figure out what answer unit(s) you want to end up with. This is usually easy.
• Write down, in math terms, everything you know that relates to the problem. You may need to read the problem several times, rephrasing parts of it, so you can translate everything into math terms. You may need to look up a few conversion factors, but that's inconvenient, not difficult.
• Pick a starting factor. If possible pick one that already has one of the units you want in the right place. Otherwise start with something you are given that is not a conversion factor.
• Plug in conversion factors that allow you to cancel out any units you don't want until you are left with only the units you do want (your answer units).
• If you can't solve the problem, pick a different starting factor and start over.
• Do the math. You may be less apt to make an error if you first multiply all the top numbers, then divide by all the bottom numbers. Now double-check your calculations.
• Ask yourself if the answer seems right or reasonable. If not, recheck everything.

Let's see how Dimensional Analysis works:

First, don't panic. If you have no idea what the answer is or how to come up with an answer, that's fine--you're not supposed to know. You're not going to solve THE problem. What you are going to do is break the problem down into several small problems that you can solve.

Here's your first problem:

1. Ask yourself, "What units of measure do I want to know or have in the answer?" In this problem you want to know "seconds in a day." After you figure out what units you want to know, translate the English into Math. Math is a sort of shorthand language for writing about numbers of things. If you can rephrase what you want to know using the word "per," which means "divided by," then that's a step in the right direction, so rephrase "seconds in a day" to "seconds per day." In math terms, what you want to know is:

2. Ask, "What do I know?" What do you know about how "seconds" or "days" relate to other units of time measure? You know that there are 60 seconds in a minute. You also know that in 1 minute there are 60 seconds. These are two ways of saying the same thing. You know that there are 24 hours in a day (and in one day there are 24 hours). If you could now connect "hours" and "minutes" together you would have a sort of bridge that would connect "seconds" to "days" (seconds to minutes to hours to days). The connection you need, of course, is that there are 60 minutes in an hour (and in one hour there are 60 minutes). When you have this kind of connection between units, then you know enough to solve the problem--but first translate what you know into math terms that you can use when solving the problem. If in doubt, write it out:

All of these statements, or conversion factors, are true or equivalent (60 seconds = 1 minute). All you need to do now is pick from these statements the ones that you actually need for this problem, so....

3. Ask, "From all the factors I know, what do I need to know?"

Remember that you want to know:

So pick from the things you know a factor that has seconds on top or day(s) on the bottom. You could pick either of the following two factors as your "starting factor:"

Write down your starting factor (say you pick 60 seconds per 1 minute):

Now the trick is to pick from the other things you know another factor that will cancel out the unit you don't want. You start with "seconds" on top. You want "seconds" on top in your answer, so forget about the seconds--they're okay. The problem is you have "minutes" on the bottom but you want "days." You need to get rid of the minutes. You cancel minutes out by picking a factor that has minutes on top. With minutes on top and bottom, the minutes will cancel out. So you need to pick 60 minutes per 1 hour as the next factor because it has minutes on top:

You now have seconds per hour, since the minutes have cancelled out, but you want seconds per day, so you need to pick a factor that cancels out hours:

4. Solve it. When you have cancelled out the units you don't want and are left only with the units you do want, then you know it's time to multiply all the top numbers together, and divide by all the bottom numbers.

In this case you just need to multiple 60x60x24 to get the answer: There are 86,400 seconds in a day.

Here's how this problem might look if it were written on a chalkboard:

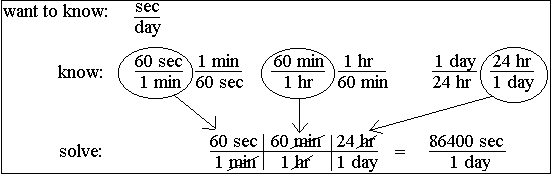
Remember that you don't need to worry about the actual numbers until the very end. Just focus on the units. Plug in conversion factors that cancel out the units you don't want until you end up with the units you do want. Only then do you need to worry about doing the arithmetic. If you set up the bridge so the units work out, then, unless you push the wrong button on your calculator, you WILL get the right answer every time.